Ratio de Sharpe

El ratio de sharpe es una medida de rendimiento de portafolios creada en 1966 por William Sharpe, ganador del premio nobel de economía en 1990, utilizada hoy en día por muchos inversionistas para comparar carteras y activos.
La finalidad de este ratio es poder comparar carteras o activos que tengan niveles de riesgo muy distintos, por ejemplo, un fondo conservador comparado con uno arriesgado, y poder ajustar sus retornos a estos distintos niveles de riesgo.
¿Por qué? No es lo mismo comparar un fondo que renta 15% al año, pero que a lo largo de ese año tuvo movimientos (ganancias o pérdidas) muy grandes versus uno que rentó 10% al año, pero que estuvo sin movimientos grandes, es decir, que fue más bien lineal.
En palabras simples, la medida calcula la rentabilidad, pero ajustada a su riesgo:
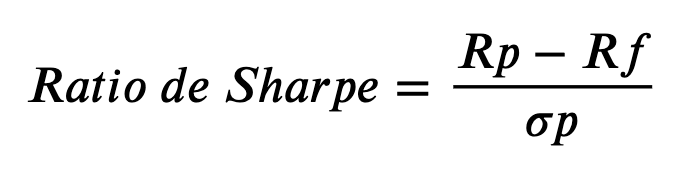
Donde:
??: Retorno anual del portafolio
??: Tasa libre de riesgo
???: Desviación estándar del portafolio
A mayor ratio de Sharpe, mejor es la rentabilidad de la cartera que estamos comparando, ya que muestra un mejor retorno sin tanta volatilidad. En cambio, si el ratio es negativo, indica que la rentabilidad del activo ha sido menor a la del libre de riesgo, por lo tanto, es más rentable invertir en activos “seguros” (como depósitos a plazo) que en este activo.
Una de las críticas que se le hace a este indicador es que ocupa la volatilidad como medida de riesgo. Para muchas personas el excesivo movimiento de un activo no lo hace tan riesgoso (ya que el movimiento puede ir sólo en sentido positivo), pero sí la probabilidad de perder plata.
En el caso del índice de sharpe, la volatilidad (representada en la desviación estándar) no diferencia entre retornos positivos o negativos, por lo que nos limita nuestra comparación a sólo “movimientos” y no de qué tipo son.
Recomendación: Nunca es bueno quedarse sólo con el resultado de un índice, más bien hay que utilizarlo junto con otros para sacar conclusiones más acertadas (dependiendo lo que estemos buscando) y poder así tener una visión menos sesgada.